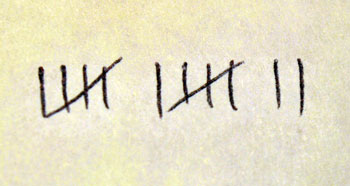Municipal Math: How Fast Can You Re-Count?
Editor’s note: This is an occasional column that presents simple math puzzles stumbled over by The Chronicle “in the wild,” while covering local government. The puzzles are meant to be accessible to kids in high school, junior high, or elementary school.
On Aug. 7, 2012, ballots were cast in primary elections – to finalize the ballot choices for voters in the Nov. 6 general election.
And last week, on Sept. 4, 2012, the Washtenaw County board of canvassers conducted a recount of some of those ballots. Several different races were recounted, including some from Augusta Township, Sylvan Township, the city of Ypsilanti, and the city of Ann Arbor.
In the city of Ann Arbor, it was the Ward 4 city council contest that was recounted. That race had offered a choice for voters between incumbent Margie Teall and Jack Eaton.
The initial count of ballots across Ward 4 showed Teall with a total of 866 votes, compared to 848 votes for Eaton. That’s a difference of 18 votes. Another way of putting that: There was an average difference of exactly two votes per precinct in Ward 4. [Warm-up puzzle: How many precincts are in Ward 4?]
In the recounted totals, each candidate lost a vote in Precinct 9. In Precinct 6, Teall picked up one vote and Eaton lost one. That left Eaton and Teall with 846 and 866 votes, respectively. So the hand-counting of the paper ballots essentially confirmed the result of the optical scanners used on election day.
I’ve now covered four recounts for The Chronicle in the last five election cycles. At a recount event, as many as four separate tables might be set up in the room. Of course, the candidates in the races being recounted and their supporters are interested in watching the recounting of the ballots – to make sure everything is done properly. So it’s typical that four or five people stand around each of the tables watching the recounting as it takes place.
The actual recounting of the ballots for a given precinct is done by three people seated at the table. One person examines each paper ballot and calls out the name of the candidate who received a vote. The two other people each record a tally mark on a grid. At the end of the recounting, the hand-recorded totals on the two grids must match each other. If they don’t, everything must be re-recounted.
So the recounting procedure depends on the ability of the talliers to hear the person who is calling out the candidate name for each ballot. Because of that, everyone in the room always observes strict silence, without even being told by members of the board of canvassers that they must be quiet.
I’m kidding. It’s always necessary for a member of the board to shush everyone – more than once. That’s because we all fall prey to the belief that we can have our own side conversations that are quiet enough not to disrupt the counting – unlike those other loudmouths.
One reason those side conversations take place is that people need a way to pass the time. That’s because watching a recount is just plain boring. (That’s how you know it’s important.) So as you’re standing there watching, you start to wonder: How long is this going to take?
And as you look at the number of people assembled in the room, some of whom are being paid $12 an hour to do the recounting, you also wonder: How much is this going to cost? [Full Story]