Municipal Math: How Tall Is the Schoolhouse?
Today marks the first day of classes for students in the Ann Arbor Public Schools and many other local districts.
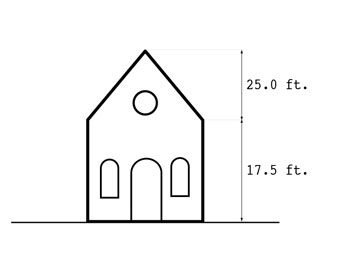
Figure 1. How tall is the schoolhouse? Note that the drawing is intentionally not to scale. Also note that the definition of “height” in Ann Arbor’s zoning code requires not just performing a sum of two numbers, but also a division.
So I’m taking advantage of the occasion to launch an occasional series that is meant to present math puzzles I’ve stumbled over “in the wild,” in the course of covering local government. It will appear only as time allows, so this could very well be the only installment of the series.
The puzzles are meant to be accessible to kids in high school, junior high, or elementary school – so for many Chronicle readers, they will be trivial.
But these puzzles might offer readers’ children a chance to apply what they’ve learned in math class to an actual, authentic real-life example – drawn from the municipal workings of the city in which they live.
Today’s puzzle has a geometric flavor. The basic question: How tall is the schoolhouse in Figure 1?
First, let’s please agree not to argue about the quality of the drawing. I admit that it may look more like a church than a schoolhouse. I took as my starting point a photograph included in a recent piece by local history columnist Laura Bien.
The drawing is not Laura’s fault, of course. The drawing differs from that photo in many ways. For example, the drawing lacks a belfry and an American flag on the roof. I left them out, because they make the math puzzle more complicated than necessary.
Another reason I left them out: The real-world example – on which the puzzle is based – was not a schoolhouse. I chose a schoolhouse for the drawing just to honor today as the first day of school. The real world-example is a two-building apartment complex called City Place, located on South Fifth Avenue, just south of William Street.
Puzzle One: How Tall?
Puzzle One: How tall is the schoolhouse in Figure 1?
A good response to this puzzle is: What do you mean by tall?
We could argue for years about what the definition of “tall” should be. Here’s what the definition of “tall” is, according to the official rules used by the city of Ann Arbor:
Building height: The vertical distance of a building measured from the average elevation of the finished grade within 20 feet of the building to the highest point of the roof for a flat roof, to the deck line of a mansard roof, or to the midpoint elevation between eaves and ridge for a gable, hip or gambrel roof of a building.
That’s a lot of words. Many of them don’t apply to our puzzle. So let’s focus on the words in bold italics:
Building height: The vertical distance of a building measured from the average elevation of the finished grade within 20 feet of the building to the highest point of the roof for a flat roof, to the deck line of a mansard roof, or to the midpoint elevation between eaves and ridge for a gable, hip or gambrel roof of a building.
The phrase “finished grade” has a special meaning in that sentence. It doesn’t mean a grade in school you completed. It basically just means the ground. And “midpoint elevation” is just a fancy way of saying “the halfway point.” So let’s summarize the parts of the definition we need:
Building height: The vertical distance measured from the ground to the half-way point between the eaves and ridge.
In Figure 1, the height between the eaves and the ridge is given as 25.0 feet.
That’s everything you need to figure out the height of the schoolhouse. If you’re so inclined, leave your solution in the comment section. Please show your work.
City Place
The dimensions given in the puzzle are the same as the dimensions of the City Place apartment buildings. That project has a long, complicated history.
Here’s one little part of that history – even though it still glosses over many details.
As the City Place project was going through the city’s approval process, people who lived in that neighborhood disagreed with the way the city calculated the height. That’s because the apartment building isn’t as simple as the schoolhouse drawing shown in the puzzle.
The apartment building actually includes a large dormer. And according to some neighbors of the City Place project, the large dormer changed the true location of the “eave” of the building. So they said that the building was actually over 35 feet tall, according to the city’s definition.
Thirty-five feet is taller than the number you should have calculated in Puzzle One. And it’s taller than what’s allowed in that area of the city.
The city didn’t change its mind about the way the height should be calculated for the building. And the two apartment buildings were constructed this past summer.
Puzzle Two: What Shape Should the Dirt Be?
There’s now a new disagreement – between the neighbor just to the north of the project and the builder of the apartments.
The disagreement stems from a change in a planned height. We’ve already solved a puzzle about building height. But as the City Place project was going through the approval process, a different kind of height changed in the project’s plans. The height that changed was not the height of the building itself, but rather the height of the building above sea level.
The earlier drawings showed the north building at an altitude of 857 feet above sea level. But some later drawings showed the north building at an altitude of 858.5 feet above sea level. That’s 1.5 feet higher.
Figure 2 shows that same kind of situation for the schoolhouse in our puzzle. In Figure 2, the schoolhouse is raised 1.5 higher, compared to sea level.
That sea-level height change has an impact for the building height calculation. Remember the part in the definition of height that says you measure from the ground? If the entire building is raised by 1.5 feet relative to sea level, as shown in Figure 2, that will increase the official height of the building according to the definition … unless we change the height of the ground around the building, too.
According to the definition, it’s not all the ground everywhere that has to be changed – just the ground within 20 feet of the building. The definition states that we have to look at the “average elevation of the finished grade within 20 feet of the building.”
So one way to do that is to pile a squared-off block of dirt 20 feet wide and 1.5 feet deep all around the building. But that would leave a 1.5-foot tall miniature “wall” 20 feet away from the building. Let’s think about other ways to add ground, that don’t have this vertical wall of dirt 20 feet away from the building.
Puzzle Two: Describe an exact shape for added ground (and its dimensions) around the schoolhouse that will keep the “height” of the schoolhouse identical to the original “height.” The shape of the added ground cannot have a vertical edge 20 feet away from the building.
If you solved Puzzle Two, then you probably came up with something similar to what the builder of the apartment complex did. Your solution likely involved a nice gentle smooth slope from the building to a point 20 feet from the building.
So what happens when rain hits a sloped surface? It runs down that surface, of course. And the neighbor to the north of City Place contends that the water is now draining onto his property – because of the added dirt. That’s now the subject of a lawsuit – because it’s not legal to cause the rainwater from your property to drain onto your neighbor’s land.
If you are so inclined (pun intended), describe your solution to Puzzle Two in the comments.
Regular voluntary subscriptions from Chronicle readers add up to help support our coverage of local government and civic affairs. Click this link for details: Subscribe to The Chronicle. And if you’re already supporting us, please encourage your friends, neighbors and colleagues to help support The Chronicle, too!


Problem 1 seems pretty straightforward, but problem 2 is a little tricky. You can’t just raise the ground level at the building by 3 feet and make a steady slope out to the previous ground level 20 feet out. That works on the sides, where “the finished grade within 20 feet of the building” forms a rectangle on each side, but not on the corners, where “the finished grade within 20 feet of the building” forms a quarter circle at each corner. The problem is that the area of a circle (including a portion of a circle) doesn’t increase linearly but exponentially. The area in the four quarter circles is 400 times pi, or about 1,256 square feet. To get a circle with half that area (about 628 square feet), you need a radius of about 14.14 feet. The result of this is that while a steady slope from 0 feet to 3 feet works on the sides, the corners will need either a steeper slope farther out, rising to a plateau, or a curved slope that increases more quickly near the outside but then becomes flatter (though not fully flat) nearer the building.
I don’t think we have enough information to figure out exactly how to accomodate this difference. If the building had a very small floor space, the quarter-circles at the corners would make up a proportionally greater portion of “the finished grade within 20 feet of the building”. To illustrate this, consider that for a hypothical building with zero floor space (a point), “the finished grade within 20 feet of the building” would simply be a circle with a 20-foot radius around the point-building, so the area would be about 1256 square feet and you’d probably need to grade the surface using an arc as mentioned above. On the other hand, for an extremely large building, say 1000 feet to a side, the total area is 81,256 square feet, and you can almost ignore the issue of the quarter-circles at the corners.
To put it another way, assuming the prior “ground level” is flat and can’t be changed, the volume of new materials (soil, rocks, etc.) in cubic feet is approximately 1885 (corners) plus 60 times the width of the building (front and back sloopes), plus 60 times the depth of the building (side slopes). If we assume dimensions of 50 by 100 feet, the total volume added to ground level needs to be 10,885 cubic feet. If we want to be jerks and make rainwater run toward one neighbor, we could build a quarter-cylindroid running along the long side of the building, rising about 6.9 feet high against the side of our building, and extending the full 20 feet out. (Volume of a quarter-cylindroid is .25 * pi * 1/2 major axis * 1/2 minor axis * “height”, giving a simple algebraic equation of .25 * pi * 20 * x * 100 = 10,885; I get x=6.9296…, or about 6 feet 11 inches.)
I suspect that Puzzle 1 (and Puzzle 2) are mislabeled or misdrawn.
As drawn in Puzzle 1, the height labeled 25 ft. is shorter than the height labeled 17.5 ft. It would also be extremely unusual for the height (top to bottom) of the gable to be more than the single-story building before it.
I suspect the intent was for the gable to add 25 ft. – 17.5 ft = 7.5 ft more to the height of the single story building, but that would require the arrow labeled 25 ft. to extend all the way to the ground.
If everything is correct as labeled, the answer to Puzzle 1 is 17.5 + (25 / 2) = 30 ft.
If however, the arrow was drawn incorrectly then the answer is 17.5 + ((25 – 17.5) / 2) = 21.25 ft.
Dave, I’m disappointed that you–a linguist, yet–conflated tallness and height. Tallness is a relative term, as in “too tall”, “not tall enough”, or “as tall as a tree”.
So, then, how tall is the schoolhouse? I’ll leave that for the CP neighbors to answer.
Re: “I suspect that Puzzle 1 (and Puzzle 2) are mislabeled or misdrawn.”
From the caption to Figure 1: “Note that the drawing is intentionally not to scale.”
Re: “It would also be extremely unusual for the height (top to bottom) of the gable to be more than the single-story building before it.” Yet these are the dimensions of the City Place buildings. So I think those who opposed construction of the project would tend to agree with the assessment of “extremely unusual.”
@5 I did reread to make sure I hadn’t missed something, butI still missed the caption. My apologies.
You don’t often make mistakes, but I caught you this time. You say, “The apartment building actually includes a large dormer.” That’s not correct. The building has no dormer and no eaves, as is clear from this photo: [photo]
What look like dormer and eaves are tacked-on decoration.
So, I’m further confused. Looking at the picture in @7, there are two stories in the first 2 floors, and essentially two stories in the center of the “dormer”. How is the former 17 ft. high and the latter 25ft. high? Aren’t they roughly the same height?
Re: [8] Here’s the drawing corresponding to the building: [.pdf of extract from City Place site plan].
@7: Thank you for the photo, and thank you for “getting it.” Indeed, this was a three-story building with a relatively flat gable roof. The height of this roof, based on the approved drawings and the City’s own height definition, was over 35 feet (the zoning limit is 30 feet in this district). As shown in the photo, a faux roof was then tacked on to the sides and peak to make the third floor of the building look like big dormers. Slots in the middle complete the illusion. City staff was completely taken in by this architectural charade and measured the building height to the middle of the tacked-on faux roof, giving a height of 30 feet. Of course, they only had drawings to go by at the time. We tried to explain what was happening–even to the point of building scale models–but only received blank stares in return.
Then, last year, the developer apparently decided he needed more ceiling height in the basement units, so he raised the level of the first floor. This change in the drawings was missed by staff, building permits were issued, and here we are with a building that is now actually over 36 feet tall, with grading that does not match the plan approved by City Council back in 2009, and a lawsuit against the City and the developer. (I’m not a party to the lawsuit, in case anyone was wondering.) The new grading should have affected the calculation of building height, but sadly, staff does not perform an averaging of the finished grade as required, but instead uses a few points at the building perimeter.
City Place is a “how-to” manual for developers interested in maximizing every conceivable dimension of their buildings above and beyond any reasonable interpretation of city code for R4C districts. Incredibly, more than three years later, there have been exactly ZERO reforms in city code or its interpretation by staff that might prevent this same thing from happening again. This in spite of the fact that multiple city council members and planning commissioners lamented loudly that these reforms were way overdue when they approved City Place.
“The Ann Arbor Public School technology bond professional team has asked that the board of trustees appropriate $54,540 to purchase 30 Macbook Pro laptop computers, in order to train and test on Apple’s new Mountain Lion operating system.”
Since there’s no way to comment on today’s Civic News Ticker item on this, I’m doing it here. (It’s math related, after all, and almost municipal in nature. Feel free to move it, Dave.)
I wonder about the $1,818 average cost ($54,540/30, there’s the math) of those laptops. I’m a software developer and considering a new 13″ Macbook Pro that’s available for $1499. Do they need 15″ screens, really? Or is the extra $200+ for something else? The model I’m looking at isn’t even at the low end, which is $1199. I didn’t look at the Macbook Air models, but the low end for those is $999 for an 11″.
Here’s a link to Apple’s quote to AAPS: [link]
Thanks, Dave. So they got $100 off (educational discount?) the base 15″ model and paid ~$600 each for the extra screen space and a slightly faster processor relative to the 13″ model with the same amount of memory and disk space. Apple did throw in an 11″ MacBook Air and a 21.5″ iMac to sweeten the deal.
I suspect that the technology bond professional team are projecting personal desires somewhat.